JBoss.orgCommunity Documentation

Chapter 4. Score calculation with a rule engine

4.1. Rule based score calculation
4.2. Defining the score rules source
4.2.1. A scoreDrl resource on the classpath
4.2.2. A RuleBase (possibly defined by Guvnor)
4.3. Implementing a score rule
4.4. Delta based score calculation
4.5. The ScoreDefinition interface
4.5.1. Implementing a custom Score
4.6. Tips and tricks

4.1. Rule based score calculation

The score calculation (or fitness function) of a planning problem is based on constraints (such as hard constraints, soft constraints, rewards, ...). A rule engine, such as Drools, makes it easy to implement those constraints as score rules.

Adding more constraints is easy and scalable (once you understand the DRL syntax). This allows you to add a bunch of soft constraint score rules on top of the hard constraints score rules with little effort and at a reasonable performance cost. For example, for a freight routing problem you could add a soft constraint to avoid the certain flagged highways during rush hour.

4.2. Defining the score rules source

There are 2 ways to define where your score rules live.

This is the simplest way: the score rule live in a DRL file which is a resource on the classpath. Just add your score rules *.drl file in the solver configuration, for example:


    <scoreDrl>/org/drools/planner/examples/nqueens/solver/nQueensScoreRules.drl</scoreDrl>

You can add multiple <scoreDrl> entries if needed, but normally you 'll define all your score rules in 1 file.

If you prefer to build the RuleBase yourself or if you're combining Planner with Guvnor, you can set the RuleBase on the XmlSolverConfigurer before building the Solver:


    xmlSolverConfigurer.getConfig().setRuleBase(ruleBase);

4.3. Implementing a score rule

The score calculation of a planning problem is based on constraints (such as hard constraints, soft constraints, rewards, ...). A rule engine, such as Drools, makes it easy to implement those constraints as score rules.

Here's an example of a constraint implemented as a score rule in such a DRL file:

rule "multipleQueensHorizontal"
    when
        $q1 : Queen($id : id, $y : y);
        $q2 : Queen(id > $id, y == $y);
    then
        insertLogical(new UnweightedConstraintOccurrence("multipleQueensHorizontal", $q1, $q2));
end

This score rule will fire once for every 2 queens with the same y. The (id > $id) condition is needed to assure that for 2 queens A and B, it can only fire for (A, B) and not for (B, A), (A, A) or (B, B). Let's take a closer look at this score rule on the starting solution of 4 queens:

Starting solution for the 4 queens puzzle

Figure 4.1. Starting solution for the 4 queens puzzle


In this starting solution the multipleQueensHorizontal score rule will fire for 6 queen couples: (A, B), (A, C), (A, D), (B, C), (B, D) and (C, D). Because none of the queens are on the same vertical or diagonal line, this starting solution will have a score of -6. An optimal solution of 4 queens has a score of 0.

4.4. Delta based score calculation

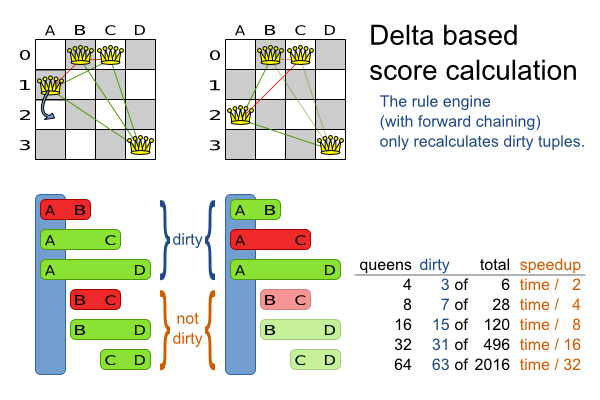
It's recommended to use Drools in forward-chaining mode (which is the default behaviour), as for score implementations this will create the effect of a delta based score calculation instead of a full score calculation on each solution evaluation. For example, if a single queen A moves from y 0 to 3, it won't bother to recalculate the "multiple queens on the same horizontal line" constraint between 2 queens if neither of those queens is queen A. This is a huge performance gain. Drools Planner gives you this huge performance gain without forcing you to write a very complicated delta based score calculation algorithm. Just let the Drools rule engine do the hard work.

Delta based score calculation for the 4 queens puzzle

Figure 4.2. Delta based score calculation for the 4 queens puzzle


The speedup due to delta based score calculation is huge, because the speedup is relative to the size of your planning problem (your n). By using score rules, you get that speedup without writing any delta code.

4.5. The ScoreDefinition interface

The ScoreDefinition interface defines the score representation. The score must a Score instance and the instance type (for example DefaultHardAndSoftScore) must be stable throughout the solver runtime.

The solver aims to find the solution with the highest score. The best solution is the solution with the highest score that it has encountered during its solving.

Most planning problems tend to use negative scores (the amount of negative constraints being broken) with an impossible perfect score of 0. This explains why the score of a solution of 4 queens is the negative of the number of queen couples which can attack each other.

A ScoreDefinition instance is configured in the solver configuration:


    <scoreDefinition>

        <scoreDefinitionType>SIMPLE</scoreDefinitionType>

    </scoreDefinition>

There are a couple of build-in ScoreDefinition implementations:

You can implement your own ScoreDefinition, although the build-in score definitions should suffice for most needs.

A ScoreCalculator instance is asserted into the working memory as a global called scoreCalculator. Your score rules need to (indirectly) update that instance. Usually you 'll make a single rule as an aggregation of the other rules to update the score:

global SimpleScoreCalculator scoreCalculator;

rule "multipleQueensHorizontal"
    when
        $q1 : Queen($id : id, $y : y);
        $q2 : Queen(id > $id, y == $y);
    then
        insertLogical(new UnweightedConstraintOccurrence("multipleQueensHorizontal", $q1, $q2));
end

// multipleQueensVertical is obsolete because it is always 0

rule "multipleQueensAscendingDiagonal"
    when
        $q1 : Queen($id : id, $ascendingD : ascendingD);
        $q2 : Queen(id > $id, ascendingD == $ascendingD);
    then
        insertLogical(new UnweightedConstraintOccurrence("multipleQueensAscendingDiagonal", $q1, $q2));
end

rule "multipleQueensDescendingDiagonal"
    when
        $q1 : Queen($id : id, $descendingD : descendingD);
        $q2 : Queen(id > $id, descendingD == $descendingD);
    then
        insertLogical(new UnweightedConstraintOccurrence("multipleQueensDescendingDiagonal", $q1, $q2));
end

rule "hardConstraintsBroken"
    when
        $occurrenceCount : Number() from accumulate(
            $unweightedConstraintOccurrence : UnweightedConstraintOccurrence(),
            count($unweightedConstraintOccurrence)
        );
    then
        scoreCalculator.setScore(- $occurrenceCount.intValue());
end

Optionally, you can also weigh your constraints differently, by multiplying the count of each score rule with its weight. For example in freight routing, you can make 5 broken "avoid crossroads" soft constraints count as much as 1 broken "avoid highways at rush hour" soft constraint. This allows your business analysts to easily tweak the score function as they see fit.

Here's an example of all the NQueens constraints written as a single rule, using multi pattern accumulates and making multipleQueensHorizontal constraint outweigh the other constraints 5 times:

// Warning: This currently triggers backwards chaining instead of forward chaining and seriously hurts performance and scalability.
rule "constraintsBroken"
    when
        $multipleQueensHorizontal : Long()
        from accumulate(
            $q1 : Queen($id : id, $y : y)
            and Queen(id > $id, y == $y),
           count($q1)
        );
        $multipleQueensAscendingDiagonal : Long()
        from accumulate(
            $q2 : Queen($id : id, $ascendingD : ascendingD)
            and Queen(id > $id, ascendingD == $ascendingD),
           count($q2)
        );
        $multipleQueensDescendingDiagonal : Long()
        from accumulate(
            $q3 : Queen($id : id, $descendingD : descendingD)
            and Queen(id > $id, descendingD == $descendingD),
           count($q3)
        );
    then
        scoreCalculator.setScore(- (5 * $multipleQueensHorizontal) - $multipleQueensAscendingDiagonal - $multipleQueensDescendingDiagonal);
end

To implement a custom Score, you 'll also need to implement a custom ScoreDefinition. Extend AbstractScoreDefinition (preferable by copy pasting HardAndSoftScoreDefinition or SimpleScoreDefinition) and start from there.

Next, hook you custom ScoreDefinition in your SolverConfig.xml:


    <scoreDefinition>

        <scoreDefinitionClass>org.drools.planner.examples.my.score.definition.MyScoreDefinition</scoreDefinitionClass>

    </scoreDefinition>

4.6. Tips and tricks

In case you haven't figured it out yet: performance (and scalability) is very important for solving planning problems. What good is a real-time freight routing solver that takes a day to find a feasible solution? Even small and innocent looking problems can hide an enormous problem size. For example, they probably still don't know the optimal solution of the traveling tournament problem for as little as 10 traveling teams.